In this article, I want to talk about a generalization that I developed a few days ago. To explain the generalization better, we shall first start with a sample problem:-
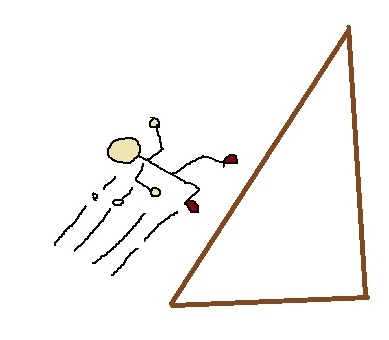
Problem) Consider a triangle with sides of 3cm, 6cm, and 8cm. A man runs around the triangle in such a way that he is always at a distance of 1cm from the sides of the triangle, then the distance travelled by him is-
The solution to the above is as follows-
First, let the take the triangle ABC. Then we draw parallel lines to all the sides to form an exterior triangle with all its sides at a distance of 1cm from the smaller triangles’ corresponding sides and curve them to form a connecting arc at the edges.

We then drop perpendiculars from each of the points ABC onto the bigger triangle on both sides of the points. Then, as we can see, since we dropped perpendiculars on both sides, the sum of the angles of angle A and the angle opposite A equals 180°.
Similarly, angle opposite B = 180° – B and angle opposite C = 180° – C.
Now the distance travelled in an arc = radius x angle subtended
In the above problem, since the man travels at a distance of 1cm from the triangle, the radius = 1cm and the angle at each corner point is 180°-A, 180°-B, 180°-C.
Therefore, the distance travelled by the man = (3+6+8) + (1)( 180°-A) + (1)( 180°-B) + (1)( 180°-C)
= 17 + 1(180°-A+180°-B+180°-C)
= 17 + 3π – (A+B+C) = 17 +3π – π = 17 + 2π
The above problem however can be generalized for an n-sides polygon, with a man running at a distance of k from the sides.
Let us take an n-sides polygon ABCD…..N. The sides of the polygon are X1, X2……, XP. A man runs around the polygon at a distance k from the sides of the polygon.
Then the angles opposite to each point become; (π-A), (π-B), (π-C)…… (π -N).
Therefore, the distance travelled = (X1+ X2+……+ XP) + (k) (π-A) + (k)(π-B) + (k)(π-C)+……+ (k)(π –N)
= (X1+ X2+……+ XP) + (k)( π-A + π-B + π-C +…… +π –N)
= (X1+ X2+……+ XP) + (k)( Nπ – (A+B+C+……+N))
= (X1+ X2+……+ XP) + (k)( Nπ – (N-2)π) [Since the sum of the
interior angles of a n-polygon = (n-2)π]
= (X1+ X2+……+ XP) + (k)(2π)
Therefore, the distance travelled by a person around any n-sided polygon at a distance k from its sides
= (X1+ X2+……+ XP) + (k)(2π)




This article presents an interesting geometric problem and its solution. The approach of drawing parallel lines and using perpendiculars is quite clever. The explanation of the distance traveled by the man around the triangle is detailed and logical. The use of angles and radii to calculate the total distance is a good application of geometric principles. How does this generalization apply to other shapes or more complex polygons?
Interesting generalization! The way you approached the problem by creating an exterior triangle and incorporating arcs is quite clever. I like how you broke down the steps to calculate the distance traveled, especially the use of perpendiculars and angles. It made the explanation easier to follow. However, I’m curious—how would this generalization apply to polygons with more sides, like a quadrilateral or pentagon? Would the method remain the same, or would it require additional adjustments? Also, do you think this approach could be extended to non-linear shapes, such as circles or ellipses? Overall, a fascinating read—I’d love to hear more about your thought process behind this! What inspired you to explore this particular problem?