In the following article we understand two different algorithms to check if a given number is prime or not in python.
Algorithm 1: –
This process is much more well known with almost every site offering this process to check if a number is prime or not. The steps are as follows: –
- Take integer input from the user.
- Take a variable to store the square root of the above user input integer (we use floor value here since the square root will be a decimal).
- Now, we divide the square root of the integer (now stored in a random variable) by all the numbers lesser than it and check if any of the numbers divide it using a for loop for the range of numbers and an if loop to check for the divisibility.
- If the divisibility is successful then the number is not prime, and the message occurs. If no number divides the integer, then the message pops up that the number is prime.
The new algorithm we will use is built on the above one and is perhaps slightly simpler to execute (the printing of the message above at the end can cause some problems if placed incorrectly in the loops, which this algorithm completely avoids).
Algorithm 2: –
- Take integer input from the user.
- Take a variable to store the square root of the above user input integer (we use floor value here since the square root will be a decimal).
- We take a variable and set its value as 2 (we will come back to why it was set to 2).
- We now use a for loop again (we can use range (2, square root variable taken earlier)) and check using an if loop if the square root variable is divisible by any number from 2 to the number just behind it.
- Each time the divisibility fails we add one to the variable taken in step 3, and if divisibility succeeds, we add 0.
- We now use another if loop and now check if the variable and the variable of step 2 is equal, if yes then original input is prime, otherwise not prime.
- Finally, we add the criteria to check if a number is a square number or not, by checking equality of the variable of step 2 squared and the input number.
We took the variable in step 4 as equal to 2 because we skip two numbers in the divisibility for loop, the number 1, and the square rooted number itself, so we must take the variable as 2. The following algorithm works because each time we do not get the divisibility criteria fulfilled, we add 1 to the variable, and a prime is not divisible by any number except 1 and itself, which we skip. Hence, if we divide by every number between 1 and the input, and not one divides it (meaning prime), it means that adding 1 each time to the variable of step 4 would finally add up the variable to the input number. This works when we take the square root instead of the input number, making the algorithm work faster.
The following is the code for algorithm 2: –
import math
x = int(input())
p = int(math.sqrt(x))
c = 2
for i in range(2,p):
if x % i != 0:
c += 1
else:
c += 0
if math.sqrt(x) == p:
print(“not prime”)
elif c == p:
print(“prime”)
else:
print(“not prime”)
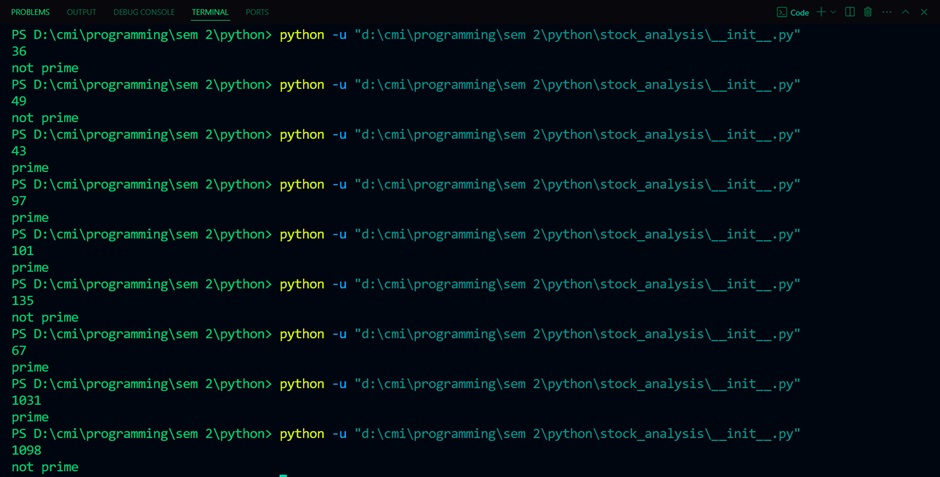
The following screenshot contains a couple of sample outputs: –
